
Most people explain AI progress with one simple idea, like Moore’s Law: more compute + more data + bigger models = smarter AI.
But this story is not just incomplete — it can also lead to the wrong strategy.
For years, the industry believed there was only one main rule behind AI improvement: pre-training scaling. While everyone focused on the visible costs of pre-training, two other (and much bigger) compute economies quietly became important.
This narrow way of thinking ignores what is actually controlling the economics and infrastructure of AI today. If we want to understand where the real demand is — and where AI is going — we must stop looking at only one curve. Instead, we must understand the three scaling laws that are reshaping the AI industry and creating a growing, hidden demand for compute.
The Foundational Law: Pre-training
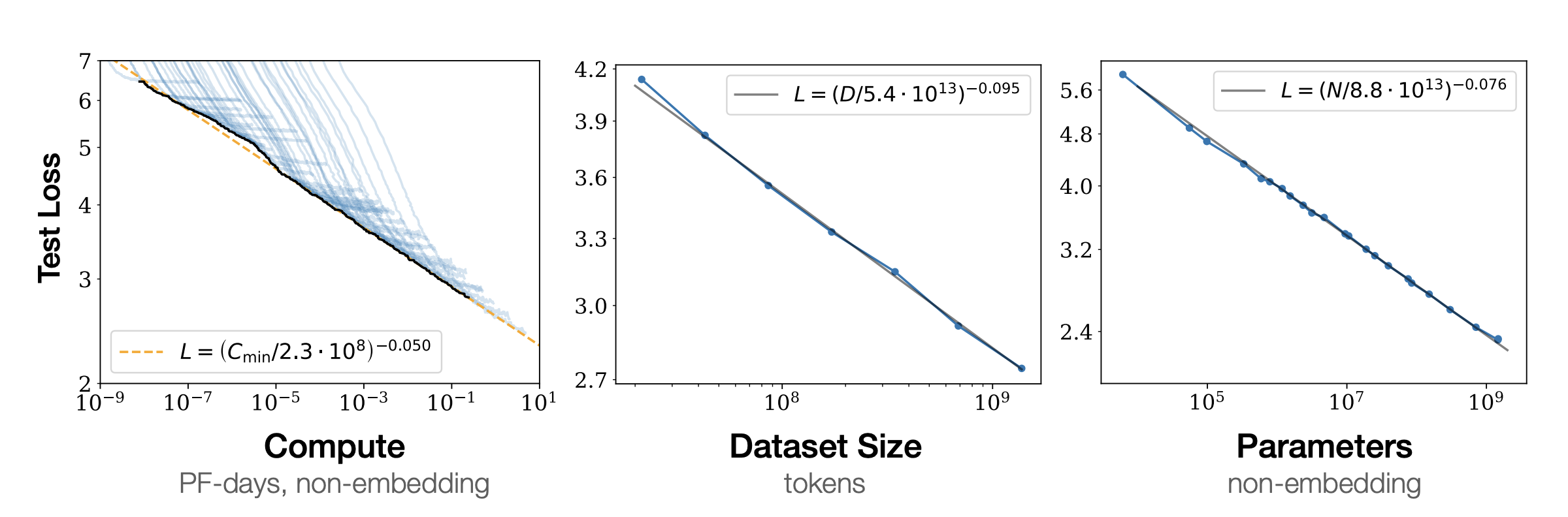
Pre-training scaling is the rule that started everything.
It means: a model becomes smarter in a predictable way when we increase all of these together:
- training dataset size
- number of model parameters
- compute used for training
This is the “more is better” approach. It created the era of huge transformer models and mixture-of-experts models, proving that pure scale can unlock powerful capabilities.
Dario Amodei, co-founder of Anthropic, describes this as a “chemical reaction.” You have three reagents, and to keep the reaction going, you must scale up all of them in proportion. If you scale up one but not the others, you run out of the other reagents, and the reaction stops. This simple but profound observation that more is better, as long as “more” applies to all three inputs is what led to the creation of today’s groundbreaking large language models.
Think of pre-training like sending an AI model to school. In school, it learns the basics:
- grammar and language structure
- relationships between ideas
- a general understanding of the world (from petabytes of data)
This law created today’s AI giants. But this first investment is only a small down payment compared to the much bigger compute cost that comes later.
The Ecosystem Multiplier: Post-training
The second law explains the huge compute growth that happens when a foundation model starts being used in the real world.
Post-training scaling means: after a model is pre-trained, we can greatly improve its performance on specific tasks using methods like:
- fine-tuning
- distillation
- reinforcement learning
The key economic point is the size of this extra demand.
Building a full ecosystem of derivative models for different use cases can take around 30 times more compute than pre-training the original foundation model.
This happens because a popular open-source model can lead to hundreds or even thousands of derivative versions, as many organizations modify it for their own needs and industries.
If pre-training is school, then post-training is specialized job training.
It gives the model domain knowledge for a specific role, like:
- understanding medical research papers
- understanding legal documents
Every new adaptation adds more compute demand. Over time, this total compute cost becomes far bigger than the original pre-training cost.
This “ecosystem multiplier” exposed a hidden layer of compute cost across the industry.
But the third law changes things even more — it changes the cost of a single thought, and turns inference from something cheap into something expensive and compute-heavy.
The Cost of a Thought: Test-time Scaling
The third and most important principle is Test-Time Scaling, also called “long thinking.”
This law says: a model can solve harder problems much better if we give it extra compute during inference, so it can think through the problem instead of giving a fast one-shot answer.
This is similar to how humans think.
- Answering “2+2” is instant
- Writing a business plan requires time, thinking, and reasoning
Test-time scaling lets AI do the same thing. It uses methods like chain-of-thought prompting, where the model breaks the problem into smaller steps and solves it step-by-step.
But this requires a lot of compute.
For difficult questions, this reasoning can take over 100 times the compute of a normal single inference pass.
This is the law that enables the next generation of agentic AI — AI systems that can do complex planning and analysis.
For example, an agentic AI could:
- analyze huge datasets to predict how a disease might progress
- optimize routes for an entire fleet of delivery trucks
Once you understand these three separate “waterfalls” of compute demand, the big question becomes:
Why does this brute-force scaling approach work so well in the first place?
The Physics of Intelligence
Scaling works because it pushes models to learn real, abstract patterns about the world — not just shallow correlations.
The reasons behind this are deep, but also practical.
Anthropic CEO Dario Amodei gives a strong analogy from physics.
He says the patterns in language and the world are like 1/f noise — a distribution with a very long tail of rare and complex patterns.
As neural networks become larger, they gain the ability to capture more of this long tail. That means they move from learning simple patterns to learning deeper themes and structures.
This connects directly to an idea from Gwern’s analysis of scaling:
the last bits are the deepest.
The long tail in Amodei’s noise distribution contains the hardest mental tasks, like:
- logic
- causality
- theory of mind
The reason “the last bits are the deepest” is that reducing the final part of prediction error forces the model to learn these rare and abstract patterns.
So brute compute works because it may be the only way to force a model to learn the huge range of complex patterns that make up real intelligence.
This gives a strong philosophical reason for brute-force scaling, which is also explained by AI pioneer Rich Sutton in “The Bitter Lesson”:
The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. … The only thing that matters in the long run is the leveraging of computation.”
— Rich Sutton, “The Bitter Lesson
The Self-Fulfilling Prophecy
AI scaling laws are very similar to Moore’s Law.
Moore’s Law was never a law of physics. It was an observation of a trend that became a self-fulfilling prophecy. The semiconductor industry used it “to guide long-term planning and to set targets for research and development.”
AI scaling now works the same way.
It has become a target that organizes huge investment across the industry. It is driven not only by technical progress, but also by human belief and economic pressure.
When one scaling curve slows down — like pre-training — the industry finds new ones to climb, like:
- post-training scaling
- test-time scaling
The investment behavior behind this is often described as a “Pascal’s wager.”
Big tech companies are investing billions because they cannot take the risk of being left behind if AI becomes the next major computing platform.
This belief is why we see projections like Dario Amodei’s idea of hundred-billion-dollar training clusters by 2027.
The belief in scaling is so strong that it is actively creating the future it predicts.
Conclusion: The New Bottleneck
The story of AI progress has changed.
It is no longer about only one scaling law that says “bigger models are better.”
Now it is about three scaling laws working together:
- pre-training
- the post-training ecosystem
- test-time reasoning
This shift has changed the industry’s main focus.
The biggest limitation is no longer about inventing new model architectures.
As Microsoft CEO Satya Nadella has pointed out, the real limiting factor is now the physical AI infrastructure itself.
All three scaling laws together are creating a never-ending hunger for compute.
More than algorithms — and even more than GPUs — the biggest bottleneck is now power availability to run these massive, energy-hungry data centers.
The next phase of AI progress will be defined less by new algorithm breakthroughs and more by the global race to build planet-scale energy and compute infrastructure that can support all three scaling laws at the same time.